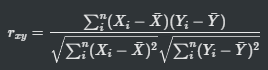어떤 상품 X와 Y, Z가 있다고 합시다. 세 상품은 속성으로 제조년도, 제조국가, 유통기한, 소비기한, 원가, 판매가 등등을 가질 수 있겠죠. 이런 속성들을 숫자로 잘 뽑으면 상품들을 속성 값들의 나열, 즉 벡터로 표현할 수 있게 됩니다. 예를 들면,
X = [1,0,2,3,2]
Y = [1,0,3,2,1]
Z = [0,1,3,1,1]
이런 식인거죠.
이렇게 아이템마다 벡터화를 해주고 나면, 아이템간 유사도를 구할 수 있습니다. 어떤 아이템이 과연 어떤 아이템과 가장 비슷한가? 혹은 비슷하지 않은가?를 계산할 수 있는 것이죠. 이 포스팅에서는 벡터를 이용하여 계산할 수 있는 유사도들을 알아보겠습니다.
1. 자카드 유사도(Jaccard Similarity)
자카드 유사도는 집합의 개념을 이용하는데요, 한줄로 정리하자면 합집합과 교집합 사이의 비율이라고 할 수 있습니다. 두 집합이 얼마나 많은 아이템을 동시에 갖고있는가?를 수치로 환산한거죠. 만약 두 집합이 함께 갖고 있는 아이템이 없다면 0, 아이템 전체가 겹치면 1로 계산이 되겠네요.
집합 X와 Y가 있다고 합시다. X=[A,B,C,D], Y=[A,C,F,G]를 값으로 갖는다고 가정하겠습니다. 합집합은 Union(X, Y) = [A,B,C,D,F,G] 이고, 교집합은 Intersection(X,Y) = [A, C] 임을 알 수 있죠. 그럼 자카드 유사도는 (교집합의 원소 개수)/(합집합의 원소 개수)로 2/6=0.33임을 알 수 있습니다.
집합을 이용하기 때문에 구현도 굉장히 단순합니다.
from math import *
def jaccard_similarity(x, y):
intersection_cardinality = len(set.intersection(*[set(x), set(y)]))
union_cardinality = len(set.union(*[set(x), set(y)]))
return intersection_cardinality / float(union_cardinality)
print(jaccard_similarity(['A', 'B', 'C', 'D'],['A', 'C', 'F', 'G']))0.3333333333333333
2. 코사인 유사도(Cosine Similarity)
코사인 유사도는 두 벡터의 코사인 각도를 계산하여 유사성을 측정합니다. 코사인 함수를 생각해보면 0도에서의 값이 1, 180도에서의 값이 -1이죠. 두 벡터가 서로 가까우면 각도가 작아서 값이 1에 가까워져 유사하다고 하고, 두 벡터가 서로 대척되면 각도가 커져서 값이 -1에 가까워져 유사하지 않다고 하는 것입니다. 벡터를 길이가 1이 되도록 정규화 시킨 후, 단위벡터간의 내적을 통해 구합니다. 정규화를 수행했기 때문에 두 벡터의 스케일 차이가 클 때 유용하게 사용할 수 있습니다.
$$cosine(X_r, X_s) = \frac{X_r \cdot X_s}{\parallel X_r \parallel \parallel X_s \parallel} = \frac{\sum_{i=1}^n X_{ri}X_{si}}{\sqrt{\sum_{i=1}^n X_{ri}^2}\sqrt{\sum_{i=1}^n X_{si}^2}}$$
import numpy as np
def cosine_similarity(a, b):
return np.dot(a, b) / (np.linalg.norm(a) * (np.linalg.norm(b)))
print(cosine_similarity([3, 10, 7, 2], [2, 15, 10, 12]))0.9031334566143822
코사인 유사도를 구하기 위해 scipy에 내장된 cosine 함수를 이용할 수도 있습니다.
from scipy.spatial.distance import cosine
print(1 - cosine([3, 10, 7, 2], [2, 15, 10, 12]))0.9031334566143822다만 cosine 함수는 코사인 유사도가 아니라 거리를 계산하기 때문에, 1에서 거리를 빼줌으로써 유사도를 구할 수 있습니다. 거리(distance)는 유사도와 대비되는 개념으로, 거리가 가깝다 = 유사도가 높다 혹은 거리가 멀다 = 유사도가 낮다 로 이해하시면 되겠습니다.
3. 피어슨 유사도(Pearson Similarity)
피어슨 유사도는 두 벡터가 주어졌을 때의 상관관계를 계산하는 것과 동일합니다. 각 벡터의 표본평균으로 normalization을 하고, 코사인 유사도를 구하면 그게 곧 피어슨 유사도 식입니다. 수식은 다음과 같습니다.
$$r_{rs} = \frac{\sum_{i=1}^n (X_{ri} - \overline{X_r}) (X_{si} - \overline{X_s})}{\sqrt{\sum_{i=1}^n (X_{ri} - \overline{X_r})^2}\sqrt{\sum_{i=1}^n (X_{si} - \overline{X_s})^2}}$$
계산된 피어슨 유사도가 1이면 양의 상관관계, -1이면 음의 상관관계, 0이면 상관관계가 없음(독립)을 의미합니다. 양의 상관관계란 비교하는 데이터 중 하나가 증가하면 다른 하나도 증가함(두 데이터가 유사하다)을 의미하고, 음의 상관관계는 하나가 증가하면 다른 하나는 감소함을 의미합니다.
수식을 이용해서 직접 함수를 작성한 방법, scipy에 내장된 pearsonr 함수를 이용한 방법, numpy에 내장된 corrcoef 함수를 이용한 방법을 이용해 피어슨 유사도를 구해보겠습니다.
from scipy.stats import pearsonr
def pearson_similarity(a, b):
return np.dot((a - np.mean(a)), (b - np.mean(b))) / ((np.linalg.norm(a - np.mean(a))) * (np.linalg.norm(b - np.mean(b))))
display(pearson_similarity([3, 10, 7, 2], [2, 15, 10, 12])
, pearsonr([3, 10, 7, 2], [2, 15, 10, 12])
, np.corrcoef([3, 10, 7, 2], [2, 15, 10, 12]))0.5756777782280114
(0.5756777782280114, 0.42432222177198864)
array([[1. , 0.57567778],
[0.57567778, 1. ]])세 방법으로 피어슨 유사도를 구한 결과, 모두 동일한 값을 갖는 것을 확인할 수 있었습니다.
참고
https://dataaspirant.com/five-most-popular-similarity-measures-implementation-in-python/
Five most popular similarity measures implementation in python
Learn the most popular similarity measures concepts and implementation in python. Euclidean distance, Manhattan, Minkowski, cosine similarity, etc.
dataaspirant.com
'繩鋸木斷水滴石穿 > 통계분석' 카테고리의 다른 글
| T-test의 개념과 R에서 적용하기 (4) | 2020.03.04 |
|---|---|
| 상관분석의 개념과 R에서 적용하기 (1) | 2020.03.03 |
| 고정효과와 임의효과 (2) | 2019.02.11 |
| 단순회귀분석(Simple Linear Regression) (0) | 2019.01.25 |